Pengukuran dan Angka Pasti

 

Pengukuran dan Angka Pasti

 

 

A.  PENGUKURAN

·      Istilah-istilah dalam pengukuran

1.    Instrumen / alat ukur

Suatu alat yang digunakan untuk menentukan nilai atau besarnya suatu kuantitas atau variabel.

2.   Ketelitian (accuracy)

Nilai yang hamper sama atau terdekat dengan pembacaan instrument terhadap nilai yang sebenarnya dari variabel yang diukur.

3.    Ketepatan (precision)

Ukuran kemampuan untuk mendapatkan hasil pengukuran yang secara berulang dari pengulangan pengukuran yang dilakukan.

Atau ukuran tingkatan yang menunjukan perbedaan hasil pengukuran pada pengukuran yang dilakukan secara berurutan.

Variabilitas biasanya dinyatakan dengan simpangan baku dan simpangan baku relatif.

4.    Sensitivitas (sensitivity)

Rasio antara sinyal keluaran atau respon instrument terhadap perubahan masukan atau variabel yang diukur.

·      Ilustrasi ketelitian (accuracy) dan ketepatan (precision) berdasarkan target

 

B  KESALAHAN DALAM PENGUKURAN

1.    Kesalahan-Kesalahan Umum (gross errors)

Disebabkan oleh kesalahan manusia, seperti kesalahan pembacaan alat ukur, kesalahan penaksiran, penyetelan yang tidak tepat, dan pemakaian instrumen yang tidak sesuai.

2.   Kesalahan-Kesalahan Sistematis (systematic errors)

Disebabkan oleh kekurangan-kekurangan pada instrumen, seperti kerusakan, terdapat bagian yang aus, pengaruh lingkungan terhadap peralatan atau pemakai.

3.    Kesalahan-Kesalahan yang Tak Disengaja (random errors)

Disebabkan oleh penyebba-penyebab yang tidak dapat secara langsung diketahui sebab perubahan-perubahan parameter atau sistem pengukuran terjadi secara acak.

·      Analisis kesalahan 

1.  Kesalahan Determinat/Kesalahan Konstan

= Mencakup kesalahan umum dan kesalahan sistematis yang berpengaruh pada akurasi/ketelitian pengukuran.

=   Dapat diatasi, ditentukan, dan diperbaiki begitu kesalahan tersebut ditemukan.

=   Contohnya :

a.  Kesalahan yang terjadi pada metode khusus yang digunakan

b. Kesalahan dalam kalibrasi dan pengoperasian peralatan pengukuran, pengotor-pengotor dalam reagen dan obat

c. Kesalahan perorangan (kesalahan dalam membaca meniscus, menuang dan mencampurkan, mengoperasikan alat timbang, memadukan warna, dan membuat perhitungan).

= Dalam farmasi, kesalahan ini dapat dihinlangkan dengan mengalibrasi alat timbang dan peralatan lain serta memeriksa perhitungan dan hasil bersama dengan praktikan lain.

2.  Kesalahan Indeterminat/Kesalahan Acak

=  Mencakup kesalahan acak yang akan mempengaruhi presisi/ketepatan.

=Terjadi secara tidak sengaja dan selalu ada.

= Tidak dapat dibiarkan atau dikoreksi karena fluktuasi alami yang terjadi pada setiap pengukuran.

=    Contohnya :

a. Menembakan peluru ke sasaran, beberapa mungkin mengenai pusat sasaran, sementara yang lain akan dihamburkan di sekeliling pusat sasaran. Namun pada analisis kimia, hasil suatu rangkaian pengujian akan menunjukan pola acak di sekitar nilai rata-rata atau nilai utama yang dikenal dengan nama rata-rata (mean).

b.Pengisian obat ke dalam sejumlah kapsul dan kapsul yang dihasilkan akan memperlihatkan variasi berat tertentu.

·  Kesalahan seperti naik turunnya suhu tidak dapat dianggap sebagai kesalahan acak, melainkan kesalahan determinat yang sering disebut kesalahan semu-acak (pseudoaccidental error) atau kesalahan determinat bervariasi (variable determinate error).

·      Kesalahan diatas dapat dikurangi dengan mengontrol kondisi melalui penggunaan penangas, dapar, kelembaban, dan tekanan. Selain itu juga dapat dengan pembacaan satuan skala secara hati-hati pada gelas ukur, timbangan, dll.

·      Kesalahan determinat bervariasi walaupun terlihat indeterminat juga dapat dikoreksi dengan analisis yang hati-hati dan perbaikan teknik praktikan.

 

C.  PRINSIP MENIMBANG

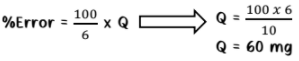
·      %Error (percent error) juga bisa ditentukan dengan rumus di bawah ini

· Sensitivity requirement/persyaratan sensitivitas adalah berat minimum yang diperlukan untuk menggerakan petunjuk sebnayak satu divisi pada skala.

·    Semakin kecil SR, semakin sensitive timbangannya.

·    Jika maksimum error 5%, maka persen kepercayaan benar 95%.

· Jika SR tidak diketahui, tentukan dengan menghitung jumlah divisi yang dilalui oleh pointer saat bergerak karena ditambahan beban 10 atau 20 mg.

Contoh :

Pointer bergerak 3 divisi saat ditambahkan beban 20 mg, SR =  = 6,67 mg

·      CONTOH SOAL 1

Berapa jumlah minimum yang dapat ditimbang pada timbangan resep Kelas A dengan potensi kesalahan tidak lebih dari 10%?

·      CONTOH SOAL 2

Jika seorang apoteker mencoba untuk menimbang 80 mg pada keseimbangan resep dengan persyaratan sensitivitas (SR) 4 mg, berapa persen kesalahan yang terkait dengan penimbangan?

·      CONTOH SOAL 3

Jika pointer/penunjuk bergerak 2 divisi ketika beban 10 mg ditempatkan pada sisi kanan keseimbangan resep, apa persyaratan sensitivitasnya (SR)?

·      LATIHAN SOAL

1.  Untuk mencapat ketelitian 92%, jumlah yang akan ditimbang harus berapa kali lebih besar dari SR timbangan?

2.  Jika 2 gram belerang ditimbang pada timbangan resep dengan SR 2 mg, berapa persen potensi kesalahannya?

D.  PRINSIP MENGUKUR VOLUME

E.  PRINSIP MENGUKUR PANJANG (Ketidakpastian)

·  Tidak ada pengukuran yang benar-benar tepat. Ada ketidakpastian yang berhubungan dengan setiap pengukuran.

·      Perkiraan ketidakpastian penting untuk dinyatakan dalam pernyataan hasil pengukuran.

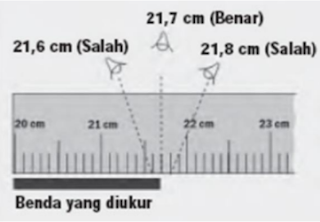
Hasil pengukuran dinyatakan 21,7 ± 0,1 cm

Hasil yang sebenarnya paling mungkin berada dalam rentang 21,6-21,8 cm

Persen ketidakpastian merupakan rasio antara ketidakpastian dengan nilai yang terukur dikalikan 100

·      Sering kali ketidakpastian pada suatu nilai terukur tidak dinyatakan secara eksplisit.

·      Ketidakpastian dianggap sebesar satu atau dua satuan dari digit terakhir yang diberikan.

=      21,7 -> ketidakpastian dianggap 0,1 (atau mungkin 0,2). Nilai sebenarnya ada dalam rentang 21,6-21,8

=      21,70 -> ketidakpastian dianggap 0,01. Nilai sebenarnya ada dalam rentang 21,69-21,71.

·      Contoh hasil pengukuran (Nilai hasil penimbangan 1 g dengan 3 timbangan berbeda)

Ulangan	Timbangan
	A	B	C
1	1,00	1,0012	1,150
2	1,10	1,0025	1,066
3	1,20	1,0005	1,155
4	0,90	0,9995	1,105
5	1,00	1,0010	1,055
Rata-rata	1,04	1,0009	1,106
Simpangan baku	0,10	0,0010	0,041

Tingkat akurasi = B, A, C

Tingkat presisi = B, C, A

Tingkat sensitivitas = B, C, A

F.  ANGKA SIGNIFIKAN (ANGKA PENTING)

·      Adalah jumlah digit yang diketahui dapat diandalkan.

·      23,21 -> 4 angka signifikan

0,062 -> 2 angka signifikan

·  Hindari keinginan untuk menulis lebih banyak digit dari jumlah digit yang diperbolehkan pada jawaban terakhir.

· Untuk mendapatkan hasil yang paling akurat, simpan satu atau dua angka signifikan tambahan selama perhitungan dan bulatkan hanya pada hasil akhir.

·      ATURAN ANGKA PENTING

1.  Semua angka yang bukan nol (0) adalah angka penting

532,46 -> 5 AP

128.769 -> 6 AP

 

2.  Angka nol (0) yang terletak di antara yang bukan nol (0) adalah angka penting

6002 -> 4 AP

50,0004 -> 6 AP

 

3.  Angka nol (0) di belakang angka bukan nol (0) yang didahului tanda koma (,) adalah angka penting

54,2400 -> 6 AP

0,360 -> 3 AP

 

4.  Angka nol (0) pada bilangan desimal yang besarnya 0<x<1 sebelum dan sesudah tanda koma (,) BUKAN angka penting

0,000250 -> 3 AP

Angka nol (0) di sebelah kiri tanda koma BUKAN angka penting

Angka nol (0) di sebelah kanan tanda koma (di antara tanda koma dan angka 2) BUKAN angka penting

Angka nol (0) sesudah angka 5 adalah angka penting

 

5.  Angka nol (0) yang terletak di belakang angka bukan nol (0) yang diberi tanda khusus BUKAN angka penting

56000 -> 5 AP

56000 -> 3 AP (Angka nol di sebelah kanan angka nol bergaris bawah BUKAN angka penting)

56000 -> 2 AP (Seluruh angka nol BUKAN angka penting)

 

6.  Notasi eksponen

3,26 x 10⁵ -> 3 AP

5 x 10⁹ -> 1 AP

6,8400 x 10⁶ -> 5 AP

 

·      ATURAN PEMBULATAN

1.    Angka yang nilainya >5

Dibulatkan di atas, contoh 6,38 -> 6,4

2.   Angka yang nilainya <5

Dibulatkan ke bawah, contoh 8,34 -> 8,3

3.    Angka yang nilainya =5

Dibulatkan ke atas jika angka sebelumnya ganjil, contoh 5,55 -> 5,6

Dibulatkan ke bawah jika angka sebelumnya genap, contoh 4,25 -> 4,2

 

·      OPERASI ANGKA PENTING

1.  Penjumlahan dan Pengurangan

Hasil dari operasi menghasilkan hanya satu angka taksiran saja dan angka penting paling sedikit

2.  Perkalian dan Pembagian

Hasil perkalian atau pembagian hanya boleh memiliki AP sebanyak bilangan yang memiliki AP paling sedikit

3.  Pemangkatan dan Penarikan Akar

Hasil dari operasi menghasilkan banyak AP yang sama dengan bilangan yang dioperasikan

4.  Perkalian dan Pembagian dengan Bilangan Eksak

Bilangan eksak = bilangan yang pasti, bulat, dan didapat dari hasil membilang

Hasil dari operasi menghasilkan banyak AP yang sama dengan bilangan hasil pengukuran

·      LATIHAN SOAL

1.  Berapa jumlah AP dari hasil pengukuran di bawah ini!

a.  142,09 -> 5 AP

b.  0,077 -> 2 AP

2.  Tentukan hasil dari pengukuran berikut

a.  28,243 x 2,6 = 73,4318 -> 73

b.  0,25 x 4,5 = 1,125 -> 1,1

Berikut adalah file pdf dengan format A5. Kamu bisa download, print, dan masukan ke binder kamu:)

!!! KLIK DI SINI !!!